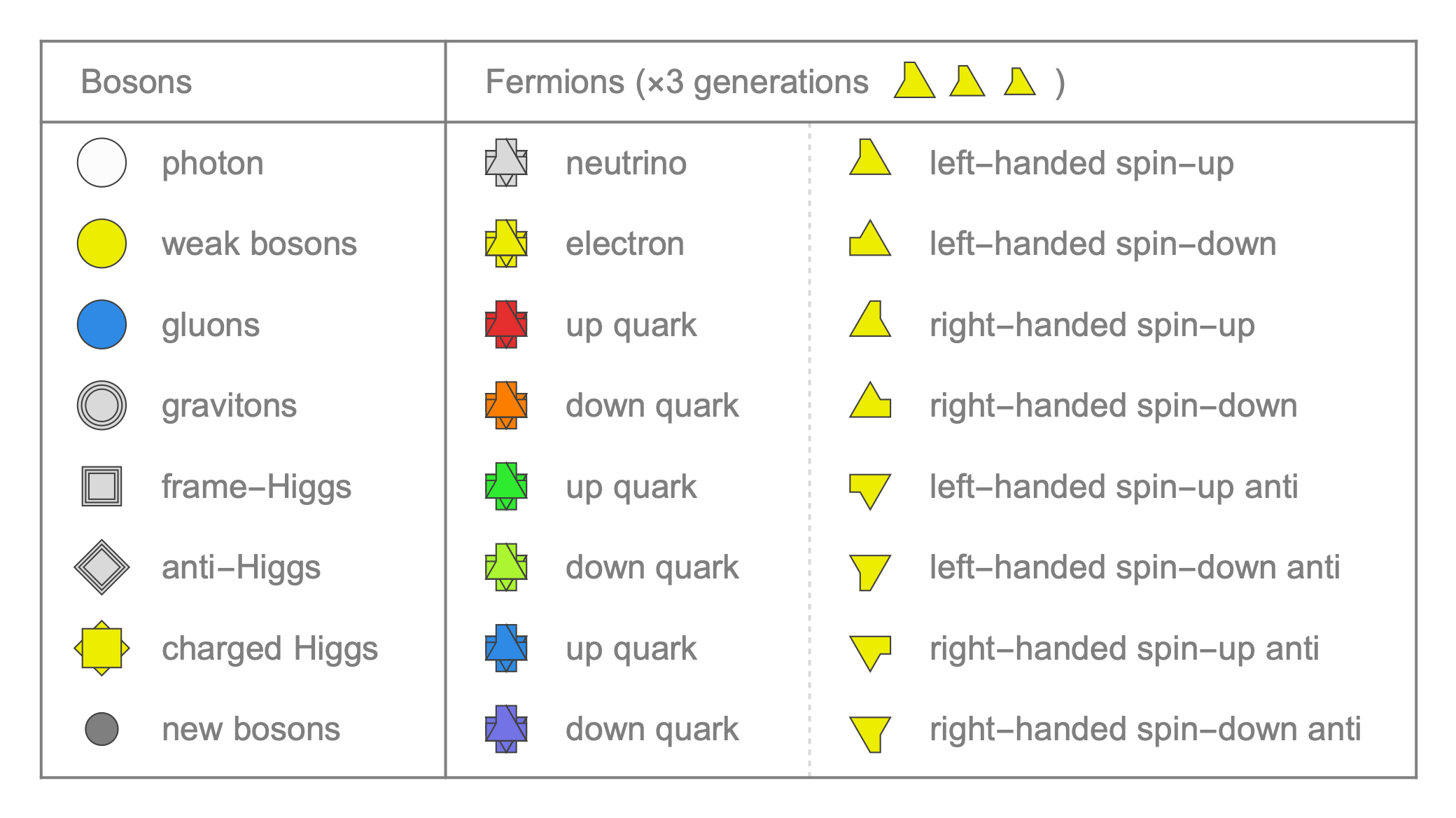
Every known elementary particle is identified by its charges with respect to the electromagnetic, weak, strong, and gravitational forces. Electrons have electric charge -1, up quarks 2/3, down quarks -1/3, and neutrinos 0, with antiparticles having opposite electric charges. In the Standard Model these electric charges are a combination of the particles' hypercharge, Y, and weak charge, W. The Elementary Particle Explorer (EPE) allows you to rotate in charge space (by dragging the image), showing the charges of all known particles. Click on them to see how they are allowed to interact, according to charge conservation.

These charges correspond to the geometry of Lie groups, and unified models of particle physics correspond to how the Lie groups of the Standard Model and gravity embed in larger Lie groups, up to the largest simple exceptional Lie group, E8. This geometry of unification is described in a recent Scientific American article and on Wikipedia, a good place to keep up with developments.
Click to start the
Elementary Particle Explorer
Elementary Particle Explorer